智酷前沿网-好玩的手机游戏大全！

网站地图
首页 评测中心正文

常见矩阵类型推荐

2025-07-06 13:55:10 投稿人 : 游客 围观 : 127 次 0 评论

矩阵是线性代数中最为基础的概念之一，广泛应用于数学、物理、计算机科学等领域。了解常见矩阵类型及其应用场景，对于提升矩阵计算效率和数据分析能力具有重要意义。本文将从矩阵基础开始，逐步介绍常见的矩阵类型，并探讨它们在实际问题中的应用。

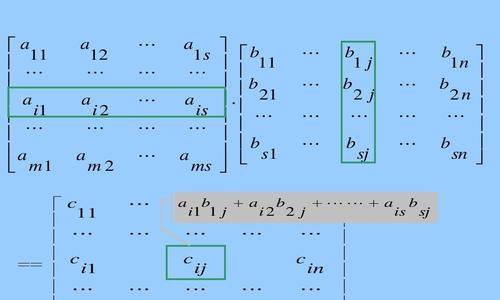
一、单位矩阵：定义和性质

单位矩阵是一个特殊的方阵，其主对角线上的元素都为1，其余元素均为0。它在线性代数中具有重要的作用，在解线性方程组、矩阵求逆等计算中起到关键作用。

二、零矩阵：特征与应用

零矩阵是所有元素都为0的矩阵，其特点在于它与其他矩阵进行相加或相乘运算时，结果仍然是零矩阵。在线性代数中，零矩阵常常用于证明某些性质或方程的解的存在性。

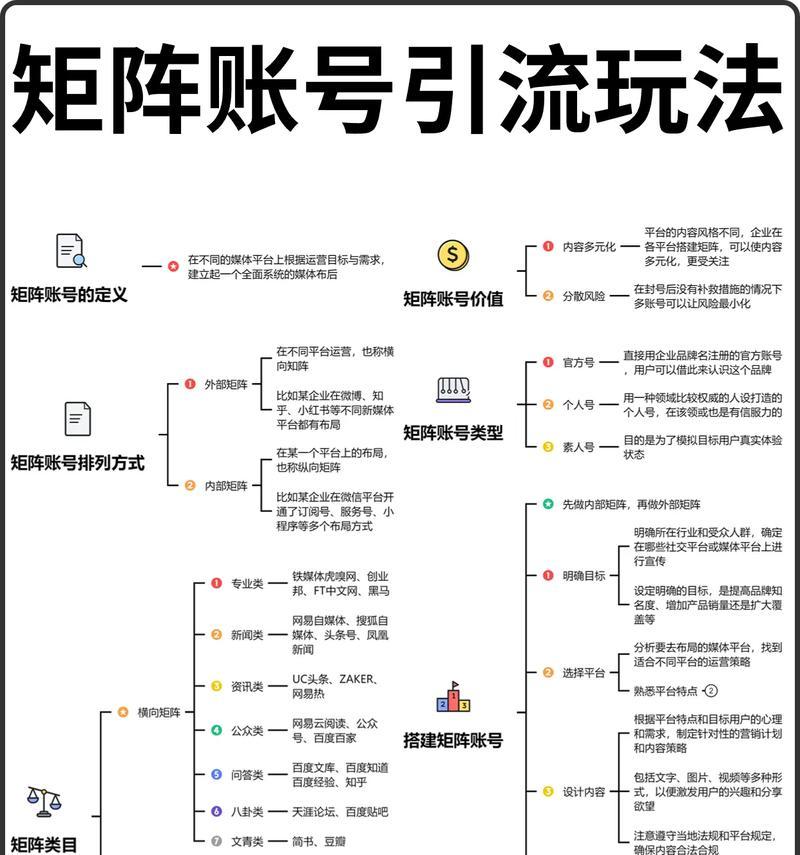
三、对角矩阵：简介与应用

对角矩阵是指除了主对角线上的元素外，其他元素均为0的矩阵。对角矩阵在许多科学领域中广泛应用，如电路分析、物体运动模拟等。

四、上三角矩阵和下三角矩阵：定义和应用

上三角矩阵是指主对角线及其上方的元素均不为0，下三角矩阵则是主对角线及其下方的元素均不为0。上三角矩阵和下三角矩阵在解决线性方程组、计算特征值等问题中具有重要作用。

五、对称矩阵与反对称矩阵：性质与应用

对称矩阵是指矩阵与其转置相等，反对称矩阵则是指矩阵与其转置相加为零矩阵。对称矩阵和反对称矩阵在物理学、经济学等领域中具有广泛的应用。

六、稀疏矩阵：定义与压缩表示

稀疏矩阵是指大部分元素为0的矩阵，相对于密集矩阵，稀疏矩阵在存储和计算上具有很大的优势。稀疏矩阵的压缩表示方法可以有效地减少内存占用和计算时间。

七、带状矩阵：特性与应用

带状矩阵是一种特殊的稀疏矩阵，它的非零元素分布在主对角线周围的一定范围内。带状矩阵在信号处理、有限元法等领域中广泛应用。

八、正交矩阵：定义与性质

正交矩阵是指其转置与逆矩阵相等的矩阵。正交矩阵在几何学、信号处理等领域中有着重要的应用，如旋转变换、数据压缩等。

九、酉矩阵：介绍与应用

酉矩阵是复数域上的方阵，其转置与共轭转置相等。酉矩阵在量子力学、通信系统等领域具有重要的应用。

十、Hermite矩阵：定义与特性

Hermite矩阵是复数域上的方阵，其转置与共轭转置相等，并满足一定的性质。Hermite矩阵在信号处理、多天线系统等领域中有重要应用。

十一、Toeplitz矩阵：简介与应用

Toeplitz矩阵是指其主对角线元素相等的矩阵，它在信号处理、图像处理等领域中具有广泛的应用。

十二、Vandermonde矩阵：定义与应用

Vandermonde矩阵是一种特殊的方阵，其列向量为等差数列的幂函数。Vandermonde矩阵在插值、函数逼近等问题中具有重要作用。

十三、半正定矩阵与正定矩阵：性质与应用

半正定矩阵和正定矩阵在优化理论、机器学习等领域中有广泛的应用。它们具有很多重要的性质，如半正定矩阵的特征值非负、正定矩阵的特征值大于零等。

十四、拟上三角矩阵和拟下三角矩阵：定义和应用

拟上三角矩阵和拟下三角矩阵是指主对角线及其相邻上方或下方的元素均不为0。它们在数值计算、线性代数等领域中具有重要的应用，如Jacobi迭代法、Gauss-Seidel迭代法等。

十五、

本文深入介绍了常见的矩阵类型，包括单位矩阵、零矩阵、对角矩阵、上三角矩阵、下三角矩阵、对称矩阵、反对称矩阵、稀疏矩阵、带状矩阵、正交矩阵、酉矩阵、Hermite矩阵、Toeplitz矩阵、Vandermonde矩阵、半正定矩阵和正定矩阵等。这些矩阵类型在数学、物理、计算机科学等领域中有着广泛的应用。通过对这些矩阵类型的了解，我们可以更好地理解和应用线性代数中的知识，提高矩阵计算效率和数据分析能力。

标签 常见矩阵类型
上一篇：坚果2.0（卓越性能、出色拍照、无与伦比的设计，打造完美用户体验） 下一篇：蘑菇街的发展现状及前景展望（探索蘑菇街的商业模式和市场表现，展望未来发展的）

相关文章

最近发表
推荐文章
小米5c值得买吗？详尽评测告诉你答案（小米5c性能优越、价格亲民，是你不容错过的选择！）

小米5c值得买吗？详尽评测告诉你答案（小米5c性能优越、价格亲民，是你不容错过的选择！）

杏雨梨云U盘教程

杏雨梨云U盘教程

快速解锁苹果手机屏幕密码的方法（秒懂，解决忘记苹果锁屏密码难题）

快速解锁苹果手机屏幕密码的方法（秒懂，解决忘记苹果锁屏密码难题）

随机文章
热评文章
标签列表