智酷前沿网-好玩的手机游戏大全！

网站地图
首页 评测中心正文

以绝对值化简的解题技巧（掌握绝对值的性质，轻松解决化简问题）

2024-08-19 11:40:01 投稿人 : 游客 围观 : 142 次 0 评论

绝对值在数学中是一个重要的概念，在解题过程中经常涉及到绝对值的化简。掌握绝对值的性质和一些常见的化简技巧，能够帮助我们在解决问题时更加高效和准确。

文章目录：

1.绝对值的定义与性质

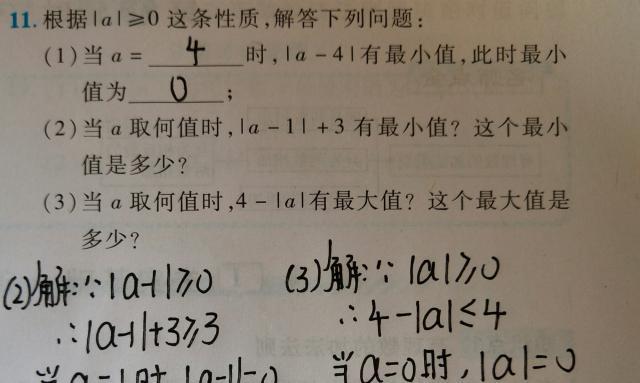
绝对值是一个数的非负值，其定义为该数与零的距离，具体表现为对于任意实数x，有|x|≥0，且|x|=x当x≥0时，|x|=-x当x<0时。此外，绝对值具有非负、不等式性、加法性、乘法性和三角不等式等性质。

2.绝对值化简基本原则

在进行绝对值的化简时，我们需要根据绝对值的性质遵循一些基本原则。这包括将绝对值中的变量与常数分开讨论、根据变量的取值范围确定绝对值内外的表达式、利用非负性化简等。

3.绝对值与加减法的化简

在进行绝对值与加减法的化简时，我们需要根据变量的取值范围进行分类讨论。当变量大于等于零时，可以直接去掉绝对值符号；当变量小于零时，需要将变量变为正数再进行计算。

4.绝对值与乘法的化简

绝对值与乘法的化简也需要根据变量的取值范围进行分类讨论。当变量大于等于零时，可以直接去掉绝对值符号；当变量小于零时，需要将绝对值中的变量变为正数再进行计算。

5.绝对值与除法的化简

绝对值与除法的化简同样需要根据变量的取值范围进行分类讨论。当变量大于等于零时，可以直接去掉绝对值符号；当变量小于零时，需要将绝对值中的变量变为正数再进行计算。

6.绝对值与指数函数的化简

绝对值与指数函数的化简也需要根据变量的取值范围进行分类讨论。当指数大于等于零时，可以直接去掉绝对值符号；当指数小于零时，需要将指数中的变量变为正数再进行计算。

7.绝对值与对数函数的化简

绝对值与对数函数的化简同样需要根据变量的取值范围进行分类讨论。当变量大于零时，可以直接去掉绝对值符号；当变量小于零时，需要将绝对值中的变量变为正数再进行计算。

8.绝对值与复合函数的化简

绝对值与复合函数的化简需要根据复合函数的具体形式进行分析和化简。在化简过程中，要注意函数的定义域和变换规律，并根据绝对值的性质进行适当的变形。

9.绝对值与不等式的化简

在解决不等式问题时，绝对值的化简是常见且重要的一步。可以通过利用绝对值的非负性质、等式性质和不等式性质来进行不等式的化简，从而得到更加简洁和易于处理的形式。

10.绝对值与线性规划问题的化简

在线性规划问题中，绝对值的化简常常出现在目标函数或约束条件中。可以根据绝对值的性质和线性规划问题的特点，将含有绝对值的问题转化为等价但更易处理的形式，从而简化求解过程。

11.绝对值化简的应用举例

通过一些具体的实例，展示绝对值化简在解题过程中的应用。从简单到复杂，逐步介绍不同类型的问题，以帮助读者更好地理解和掌握绝对值化简的技巧。

12.绝对值化简中的常见误区

分析绝对值化简过程中容易出现的常见误区和错误，包括对绝对值性质的理解不透彻、对变量取值范围判断错误等，并给出相应的解决方法和注意事项。

13.绝对值化简的解题步骤

绝对值化简的解题步骤，包括确定变量取值范围、根据变量的正负情况进行分类讨论、根据绝对值的性质进行化简等，以帮助读者在实际解题中有条不紊地进行化简。

14.深入理解绝对值的性质与化简技巧

深入探讨绝对值的性质和化简技巧，包括更复杂的问题和更高级的应用。通过理论分析和实例演示，提高读者对绝对值化简的理解和运用能力。

15.掌握绝对值化简的技巧，化繁为简解题轻松无忧

通过学习和掌握绝对值化简的技巧和方法，我们能够在解题过程中化繁为简，解决一些看似复杂的问题。绝对值化简不仅在数学中有广泛的应用，也是培养逻辑思维和分析问题能力的重要途径。

标签 绝对值化简
上一篇：三星S7Edge7.0系统更新带来的新功能与改进（全面升级，体验更畅快） 下一篇：小米4c摄像头像素表现如何？（深度分析小米4c摄像头像素及其影响因素）

相关文章

最近发表
推荐文章
小米5c值得买吗？详尽评测告诉你答案（小米5c性能优越、价格亲民，是你不容错过的选择！）

小米5c值得买吗？详尽评测告诉你答案（小米5c性能优越、价格亲民，是你不容错过的选择！）

杏雨梨云U盘教程

杏雨梨云U盘教程

快速解锁苹果手机屏幕密码的方法（秒懂，解决忘记苹果锁屏密码难题）

快速解锁苹果手机屏幕密码的方法（秒懂，解决忘记苹果锁屏密码难题）

随机文章
热评文章
标签列表